Support vector machines
Please note
It might take a couple of seconds before the mathematical notation is correctly loaded into your web browser.
1.1 Decision boundary
The support vector machine (or, abbreviated, “SVM”) is a numerical classifier. It is one of the best “off-the-shelf” supervised learning algorithms because of its practical simplicity and computational efficiency (compared to, for instance, artificial neural networks). Given a training set \(S = \{(x^{(i)},y^{(i)}), i = 1 \space , …, \space m \}\), where each example belongs to either a positive or negative class \(y^{(i)} \in \{-1, +1\}\), a SVM training algorithm builds a model that assigns new examples to one category or the other. It does so by means of a linear decision boundary. This linear decision boundary is defined by a line in 2D, a plane in 3D or a hyper plane in higher dimensional feature space, as follows:
\begin{align} f(x) = w^{T}x+b = 0 \Leftrightarrow \sum_{i = 1}^{n} w_{i}x_{i} + b = 0 \tag{1-1} \label{1-1} \end{align}
where \(n\) is the number of features in our dataset, \(x \in \mathcal{R}^n\) is a column vector of feature values, \(w \in \mathcal{R}^n\) is a column vector of weights that is normal to the separating hyperplane and \(b \in \mathcal{R}\) is the bias term, without it, the classifier will always go through the origin.
Clearly, a new set of feature values \( x^{*} \) lays on the linear decision boundary if it satisfies Equation \eqref{1-1}. Similarly, it will lay above the decision boundary if \(f(x^{*}) > 0\) and below the decision boundary if \(f(x^{*})<0\). Consequently, the prediction rule \(h(x^{*})\) is given by the sign of \(f(x^{*})\). That is, a training example is classified as either a positive or a negative class, as such:
\begin{align} h(x^{*})= \tag{1-2} \label{1-2} \begin{cases} 1 & \quad \text{if } w^{T}x^{*}+b \geq 0 \newline -1 & \quad \text{if }w^{T}x^{*}+b < 0 \newline \end{cases} \end{align}
For now, we assume that the data is linearly seperatable. In such an environment, many possible linear seperators exist. Figure 1 provides two different kinds of linear seperators, dividing the positive class, denoted with crosses, from the negative class, denoted with circles.
Figure 1: Different possible linear seperators
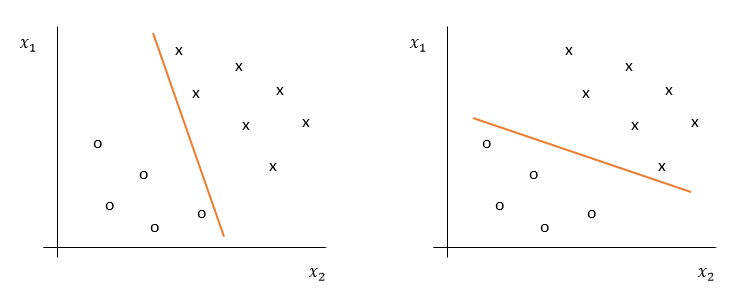
The SVM, however, has a special kind of decision boundary. In contrast to the decision boundaries demonstrated in Figure 1, the SVM assures that the decision boundary is maximally far away from any data point. The distance from the decision boundary to the closest data point determines the so-called margin of the classifier, as shown in Figure 2.
Figure 2: The maximum margin decision boundary of a SVM
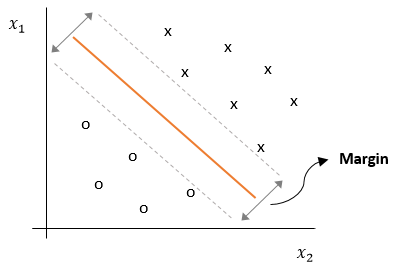
Intuitively, a classifier with a larger margin makes fewer low certainty classification decisions. That is, if we are asked to make a class prediction of a training example close to the decision boundary, this would reflect an uncertain decision. In particular, a small distortion of the feature values could change the outcome of our prediction. By maximizing the margin, we reduce the need to make these kind of low certainty decisions and provide ourselves with some sort of safety margin.
To achieve the goal of maximizing the margin, we first introduce two concepts: the functional margin and the geometric margin. While the latter provides us with a valid optimization objective, the former allows us to simplify it.
1.2 Functional margin
Given a training example \((x^{(i)}, y^{(i)})\), we define the functional margin with respect to the training example as:
\begin{align} \hat{\gamma}^{(i)} = y^{(i)}(w^{T}x^{(i)}+b) \Leftrightarrow y^{(i)}f(x^{(i)}) \tag{1-3} \label{1-3} \end{align}
Note that, according to the decision rule of Equation \eqref{1-2}, if \(y^{(i)} = 1\) then we need \(f(x^{(i)})\) to be large and positive in order for the prediction to be correct and confident (i.e. far away from the decision surface). Similarly, if \(y^{(i)} = -1\), we need \(f(x^{(i)})\) to be a large negative number for our prediction to be confident and correct. Overall, when \(\hat{\gamma}^{(i)}\) is large and positive this represents a correct and confident prediction.
Is this a valid optimization objective to achieve the optimal margin classifier? Unfortunately not, because the functional margin is underconstrained. To elaborate, note that if we multiply \(w\) and \(b\) by some constant \(c\), the decision surface nor the sign of the output will change (check in desmos). In other words, the decision rule is unaffected by scaling of the parameters. However, if we multiply \(w\) and \(b\) by some constant \(c\), the functional margin does get multiplied by that same constant. Thus, we can make the functional margin as large as we please by simply exploiting our freedom to scale \(w\) and \(b\), without affecting the actual decision boundary. This scaling property clearly implies that the functional margin is an invalid optimization objective. Nevertheless, it will come in handly later on.
We also define the functional margin with respect to the training set \(S\) as the smallest of the functional margins of the individual training examples. Denoted by \(\hat{\gamma}\), this can therefore be written:
\begin{align} \hat{\gamma} = \min_{i = 1,…,m} \hat{\gamma}^{(i)} \tag{1-4} \end{align}
1.3 Geometric margin
To define the geometric margin, we look at the Euclidean distance from any point \(\vec{x}^{(i)}\) of the training set \(S\) to the linear decision boundary. We know that the shortest distance between a point and a hyperplane is perpendicular (at 90°) to the plane. This perpendicular vector, pointing between \(\vec{x}^{(i)}\) and the decision boundary, is denoted by \(\vec{r}^{(i)}\) in Fig. 3. To stay consistent with our notation, we denote the magnitude of this vector as \(\gamma^{(i)}\) ( i.e. \(|\vec{r}^{(i)}| = \gamma^{(i)}\)). Now, taken into account that the normal vector \(\vec{w}\) is also perpendicular to the plane, \(\vec{r}^{(i)}\) and \(\vec{w}\) have the exact same direction. Consequently, we can the express the vector \(\vec{r}^{(i)}\) as:
\begin{align} \vec{r}^{(i)} = \gamma^{(i)} \hat{w} \tag{1-5} \label{1-5} \end{align}
where \(\gamma^{(i)}\) and the unit normal vector \(\hat{w}\) capture the correct magnitude and direction of the vector \(\vec{r}^{(i)}\), respectively.
Figure 3: The normal \(\hat{w}\) and \(\vec{r}\) are parallel
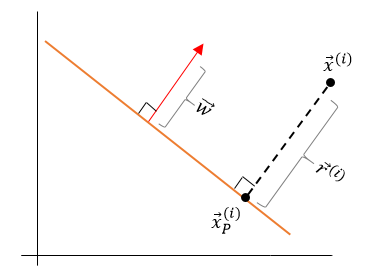
Let us label the point on the hyperplane closest to \(\vec{x}^{(i)}\) as \(\vec{x}^{(i)}_{P}\). Following the rules of vector addition we get,
\begin{align}
\vec{x}^{(i)}_P = \vec{x}^{(i)} - y^{(i)} * \vec{r}^{(i)} \tag{1-6} \label{1-6}
\end{align}
Note that we multiply \(\vec{r}^{(i)}\) by \(y^{(i)} \in \{1,-1\}\) to capture the desired sign of the operation. In particular, \(\vec{x}^{(i)}_{P} = \vec{x}^{(i)} + \vec{r}^{(i)}\) if \(\vec{x}^{(i)}\) lays below the decision boundary and \(\vec{x}^{(i)}_P = \vec{x}^{(i)} - \vec{r}^{(i)}\) if it lays above the plane.
Now, substituting \eqref{1-5} into \eqref{1-6} and writing out the unit normal gives,
\begin{align}
\vec{x}^{(i)}_P = \vec{x}^{(i)} - y^{(i)} * \gamma^{(i)} * {\frac{\vec{w}}{|\vec{w}|}} \tag{1-7} \label{1-7}
\end{align}
Moreover, \(\vec{x}^{(i)}_P\) lies on the decision boundary and so satisfies Equation \eqref{1-1}. Substititon therefore yields,
\begin{align}
\vec{w}^{T} * (\vec{x}^{(i)} - y^{(i)} * \gamma^{(i)} * {\frac{\vec{w}}{|\vec{w}|}})+b=0 \tag{1-8} \label{1-8}
\end{align}
Multiplying out the brackets of Equation \eqref{1-8} yields,
\begin{align}
\vec{w}^{T} \vec{x}^{(i)} - y^{(i)} * \gamma^{(i)} * \frac{\vec{w}^{T}\vec{w}}{|\vec{w}|}+b=0 \tag{1-9} \label{1-9}
\end{align}
Substituting \(\vec{w}^{T}\vec{w} = |\vec{w}|^{2}\) into Equation \eqref{1-9} and simplifying gives,
\begin{align}
\vec{w}^{T} \vec{x}^{(i)} - y^{(i)} * \gamma^{(i)} * |\vec{w}|+b=0 \tag{1-10} \label{1-10}
\end{align}
Finally, solving Equation \eqref{1-10} for \(\gamma^{(i)}\) gives the geometric margin of an individual training example,
\begin{align}
\gamma^{(i)} = y^{(i)} \frac{\vec{w}^{T}\vec{x}^{(i)}+b}{|\vec{w}|} \tag{1-11} \label{1-11}
\end{align}
Clearly, we cannot maximize the margin with respect to every training point. Instead, we maximize the margin with respect to the closest points to the line. If we define \(\gamma\) as the distance between the decision boundary and the point closest to it, then
\begin{align}
\gamma = \min_{i = 1, …, m}\gamma^{(i)} \tag{1-12} \label{1-12}
\end{align}
From this, we find the values for the parameters \(w\) and \(b\) which assure that \(\gamma\) is as big as possible, subject to the fact that the distance from the decision boundary to every training example is larger than or equal to the point closest to it. That is, we can extract the optimal geometric margin classifier as:
\begin{equation} \begin{array}{rrclcl} \displaystyle \max_{w, b} && \gamma \tag{1-13} \label{1-13} \newline \textrm{subject to} & \text{ } & y^{(i)} (\vec{w}^{T}\vec{x}^{(i)}+b) / |\vec{w}| \geq \gamma & \forall i = 1, …, m \newline \end{array} \end{equation}
The points closest to the separating hyperplane are called the support vectors. The optimal geometric margin classifier of Equation \eqref{1-13} produces the margin with the maximum width of the band that can be drawn separating the support vectors of the two classes.
The maximization procedure forces the training examples to be correctly labelled, because we multiplied by \(y^{(i)}\) in Equation \eqref{1-6}. In particular, misclassifications will produce negative values of \(\gamma\), which opposes the optimization objective.
Before we continue, it is worth noting that that the geometric margin is invariant to rescaling of the parameters. That is, if we replace \((w, b)\) with \((2w, 2b)\), then the geometric margin does not change. This is due to the normalization parameter in the denominator. This will come in handy later, as it allows us to impose an arbitrary scaling constraint on the parameters without changing anything important.
1.4 Primal form
The above optimization has a non-convex constraint, which we cannot plug into standard optimization software to solve. Instead, we consider an alternative:
\begin{align} \displaystyle \max_{w, b} && \hat{\gamma}/|w| \tag{1-14} \label{1-14}\newline \textrm{subject to} & \text{ } & y^{(i)}(w^{T}x^{(i)} + b) \geq \hat{\gamma} & \quad{} \forall i = 1, …, m \newline \end{align}
Here, we are maximizing \(\hat{\gamma}/|w|\), subject to the functional margins being at least \(\hat{\gamma}\). This is equivalent to the earlier optimization since the geometric and functional margin are related by \(\gamma = \hat{\gamma}/|w|\). This allow us to get rid of the non-convex constraint. However, we still have a nasty non-convex objective function. Now, taken into account that we can add an arbitrary scaling constraint on \(w\) and \(b\) without changing anything important, we will introduce the scaling constraint that the functional margin of \(w\), \(b\) with respect to the training set must be 1:
\begin{align}
\hat{\gamma} = 1 \tag{1-15} \label{1-15}
\end{align}
Since multiplying \(w\) and \(b\) by some constant \(c\) results in the functional margin being multiplied by that same constant, this is indeed a scaling constraint, and can be satisfied by rescaling \(w\), \(b\). Per our earlier discussion, this leaves both the geometric margin and decision boundary unaffected. Thus, plugging this into our problem above, and noting that maximizing \(1/|w|\) is the same thing as minimizing \(|w|^{2}\), we now have the following optimization problem:
\begin{equation} \begin{array}{rrclcl} \displaystyle \min_{w, b} && \frac{1}{2} |w|^{2} \tag{1-16} \label{1-16}\newline \textrm{subject to} & \text{ } & y^{(i)} (w^{T}x^{(i)} + b) \geq 1 & \forall i = 1, …, m \newline \end{array} \end{equation}
The above equation is an optimization problem with a convex quadratic objective and only linear constraints. Its solution gives us the optimal margin classifier and can be obtained using QP software.
Chapter 2: The soft-margin primal form
2.1 Regularization
It is worth noting that the SVM is being implicitly regularized because we are minimizing \(|w|^{2}\). This results in relatively small parameters. In turn, small changes of feature values will not result in large changes in the output values. Hence, preventing overfitting. This will come in handy once we introduce non-linearity through kernelization.
The algorithm, however, is still prone to outliers. For example, the figure below demonstrates what happens to the optimal margin classifier once we add a single outlier in the the lower-left region. As can be observed, it causes the decision boundary to migrate while substantially reducing the width of its margin. Taking this to the extreme, if the outlier would lay even further to the lower-left region, the data would become linearly inseperatable.
Figure 4: Effect of outliers on maximum margin classifier with high \(C\) (left) and low \(C\) (right)
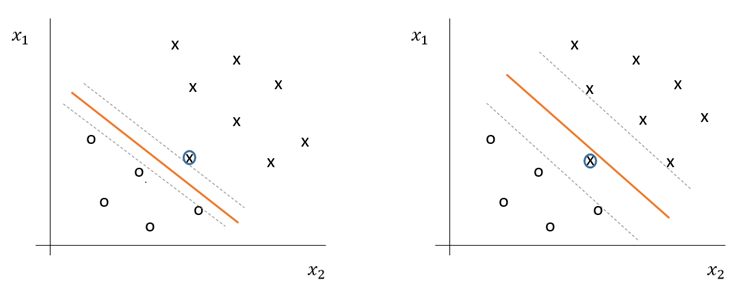
To make the algorithm less sensitive to outliers and work for non-linearly separable datasets, the optimization is reformulated using ℓ1-regularization as follows,
\begin{equation} \begin{array}{rrclcl} \displaystyle \min_{w, b, \xi_i} && \frac{1}{2} |w|^{2} + C \sum_{i=1}^{m} \xi_i\tag{2-1} \label{2-1} \newline \textrm{subject to} & \text{ } & y^{(i)} (w^{T}x^{(i)} + b) \geq 1 - \xi_i & \forall i = 1, …, m \newline && \xi_i \geq 0 & \forall i = 1, …, m \newline \end{array} \end{equation}
where \(\xi_{i}\) are non-negative variables that allow training examples to be on the wrong side of their margin as well as the decision boundary and \(C\) is a regularization parameter which controls the relative weighting between training accuracy and the mildness (and width) of the margin. The former is achieved with a high value for \(C\), and the latter with a low value for \(C\). The desired value of \(C\) is generally found using cross-validation.
2.2 Hinge loss function
From Equation \eqref{2-1}, it is worth noting that the constraint \(y^{(i)} (w^{T}x^{(i)} + b) \geq 1 - \xi_i\), which is equivalent to \(\xi_{i} \geq 1-y^{(i)} (w^{T}x^{(i)} + b)\), together with \(\xi_i \geq 0\), can be written more concisely. Particularly, because we are are minimizing \(\xi_{(i)}\), and the smallest value that satisfies the constraint occurs at equality,
\begin{align}
\xi_{i} = \max(0,1-y^{(i)} (w^{T}x^{(i)} + b)) \tag{2-2} \label{2-2}
\end{align}
Hence, the learning problem of Equation \eqref{2-1} is equivalent to the unconstrained optimization problem over \(w\),
\begin{align}
\min_{w} \frac{1}{2} |w|^{2} + C \sum_{i=1}^{m} \max(0,1-y^{(i)} (w^{T}x^{(i)} + b)) \tag{2-3} \label{2-3}
\end{align}
The last part of this equation is called the hinge loss function, which is defined as
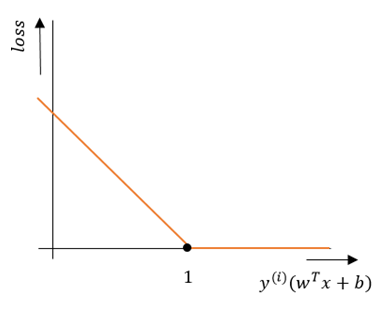
\begin{align} \mathcal{L}(x^{(i)}, y^{(i)}) = \max(0,1-y^{(i)} (w^{T}x^{(i)} + b)) \tag{2-4} \label{2-4} \end{align}
Note that, if a training example has \(y^{(i)} (w^{T}x^{(i)} + b) < 1\), then this point violates the margin constraint and therefore contributes to the loss. In contrast, if \(y^{(i)} (w^{T}x^{(i)} + b) \geq 1\), then there is no contribution to the loss. Hence, the hinge loss function \(\mathcal{L}(x^{(i)}, y^{(i)})\) is so-called piece-wise linear. This is demonstrated in Figure 5.
Figure 5: Hinge loss function is piece wise linear
2.3 Solving soft margin primal form
Now, using the hinge loss function we can rewrite the cost function of Equation \eqref{2-3} as,
\begin{align}
\mathcal{C} = \frac{1}{2} |w|^{2} + C \sum_{i=1}^{m} \mathcal{L} (x^{(i)}, y^{(i)}) \tag{2-5} \label{2-5}
\end{align}
To apply gradient descent to this cost function, the function has to be differentiable. Clearly, because we cannot take the derivative at the point where \(y^{(i)}(w^{T}x + b) = 1 \) (see Fig. 4), the hinge loss function is non-differentiable. However, we can calculate the subderivative of the hinge loss function, as such
\begin{align} \frac{d}{dw} \mathcal{L}(x^{(i)}, y^{(i)}) = \tag{2-6} \label{2-6} \begin{cases} -y^{(i)}x^{(i)} & \quad \text{if } y^{(i)} (w^{T}x^{(i)} + b) < 1\newline 0 & \quad \text{else}\newline \end{cases} \end{align}
Now, using the above equation and noting that the derivative of a sum is equal to the sum of its derivatives, we can calculate the gradient of Equation \eqref{2-5} as follows,
\begin{align} \nabla_{w} \mathcal{C} &= \frac{1}{2}\frac{d}{dw}|w|^{2} + C \sum_{i=1}^{m} \frac{d}{dw} \mathcal{L}(x^{(i)}, y^{(i)}) \tag{2-7} \label{2-7} \newline &\quad{} = w + C \sum_{\substack{i = 1 \newline s.t. \newline y^{(i)}f(x^{(i)}) <1}}^{m} y^{(i)}x^{(i)} \end{align}
Finally, using the above gradient, we can express the iterative update as,
\begin{align} w_{(t+1)} &= w_{(t)} - \eta \nabla_{w_{(t)}} \mathcal{C} \tag{2-8} \label{2-8} \end{align}
where \(\eta\) is defined as the learning rate.
Note that the cost function of Equation \eqref{2-5} consists of the sum of two convex functions. Taken in mind that the sum of two convex functions is convex, we can apply gradient descent to find the global optimal parameter values.
Chapter 3: Dual form
3.1 Dual optimization
To be able to efficiently work with non-linear data, we need to apply the so-called kernel trick (see Section 4). The primal problem is not ready to be kernelised, however, because its dependence is not only on inner products between data-vectors. To achieve this, we transform to the dual formulation by first writing the primal soft-margin optimization problem of Equation \eqref{2-1} using a generalized Lagrangian,
\begin{align} L (w, b, \xi, \alpha, \beta) = \frac{1}{2} |w|^{2} + C \sum_{i}^{m} \xi_{i} + \sum_{i}^{m} \alpha_{i} [(1 - \xi_{i}) - y^{(i)} (w^{T} x^{(i)} + b)] + \sum_{i}^{m} \beta_{i} (-\xi_{i}) \tag{3-1} \label{3-1} \end{align}
where \(\alpha_i\) and \(\beta_i\) are Lagrange multipliers that capture the inequality constraints of the regularized primal optimization problem. Now, consider the quantity,
\begin{align} \theta_P(w,b,\xi): \max_{\substack{\alpha, \beta \newline \alpha_i \geq 0, \beta_i \geq 0}} \quad{} L(w, b, \xi, \alpha, \beta) \tag{3-2} \label{3-2} \end{align}
where the subscript \(P\) stands for primal. Note that, if the constraint \(\xi_i \geq 0\) is violated (i.e. \(\xi_i < 0\) in the above maximization problem), then the adversary is free to inflate the value of \(\beta_i\) when maximizing the Lagrangian with respect to beta. In turn, causing the sum in the last term of \eqref{3-1} to become \(+\infty\). Similarly, if the margin constraint \(y^{(i)}(w^{T}x^{(i)} + b) \geq 1-\xi_i\) is violated (i.e. \([(1 - \xi_i) - y^{(i)}(w^{T}x^{(i)} + b)] > 0\)), then the adversary is free to set \(\alpha_{i}\) to a very large positive value when maximizing the Lagrangian with respect to alpha. In turn, causing the sum in the third term of Equation \eqref{3-1} to become \(+\infty\). On the other hand, taken into account that the alphas and betas are constrained to be non-negative, if both the constraints hold, the best values for \((\alpha_i, \beta_i)\) that the adversary can find are \((0,0)\). Thus, if non of the constraints are violated for all \(i = 1, …, m\), the last two terms of equation \eqref{3-1} disappear. It follows that, for a given \(w\), \(b\) and \(\xi\), we have
\begin{align} \theta_P(w,b,\xi) = \tag{3-3} \label{3-3} \begin{cases} \frac{1}{2}|w|^{2} + C \sum_{i}^{m} \xi_i & \text{if primal constraints hold} & \forall i = 1, …, m \newline \infty & \text{otherwise} \newline \end{cases} \end{align}
Thus, if the constraints do not hold, the adversary can penalize us by making the objective function arbitrarily large. Consequently, when minimizing Equation \eqref{3-3} with respect to the parameters \((w, b, \xi)\), the algorithm will always select parameters which satisfy the constraint. Hence, the minimization problem
\begin{align} \min_{w, b, \xi} \theta_P(w,b, \xi) = \min_{w, b, \xi} \max_{\substack{\alpha, \beta \ \alpha_i \geq 0, \beta_i \geq 0}} L(w, b, \xi, \alpha, \beta) \tag{3-4} \label{3-4} \end{align}
is equivalent to the primal problem of Equation \eqref{2-1}.
Now, we can also work the other way around by first minimizing with respect to the parameters \((w, b, \xi)\) and subsequently maximizing with respect to \((\alpha, \beta)\). That is, we define
\begin{align}
\theta_{D} (\alpha,\beta): \min_{w, b, \xi} L(w, b, \xi, \alpha, \beta) \tag{3-5} \label{3-5}
\end{align}
where the subscript \(D\) stands for dual. Then the dual optimization problem is given by
\begin{align}
\max_{\substack{\alpha,\beta \newline \alpha_i \geq 0, \beta_i \geq 0}} \theta_D(\alpha,\beta) = \max_{\substack{\alpha,\beta \newline \alpha_i \geq 0, \beta_i \geq 0}} \min_{w, b, \xi} L(w, b, \xi, \alpha, \beta) \tag{3-6} \label{3-6}
\end{align}
Taken into account that “max min” is always less than or equal to the “min max” of a function, we have the following inequality between the outcomes of the primal and the dual optimization problem,
\begin{align}
\max_{\substack{\alpha,\beta \newline \alpha_i \geq 0, \beta_i \geq 0}} \theta_D(\alpha,\beta) \leq \min_{w, b} \theta_P(w,b) \tag{3-7} \label{3-7}
\end{align}
That is, often a duality gap arises between the outcomes of the primal and dual problem. However, it can be shown that if the objective function is quadratic convex and the constraints are affine (that is, linear including a bias term), then the duality gap is always zero, provided one of the primal or dual problems is feasibile.* Taken into account that the objective function and constraints of the primal problem as shown in Equation \eqref{3-4} is QP, this implies that strong duality holds and the duality gap is zero. That is, there exists \(w^{*}\), \(b^{*}\), \(\xi^{*}\), \(\alpha^{*}\) and \(\beta^{*}\) such that \(w^{*}\), \(b^{*}\) and \(\xi^{*}\) are the solution to the primal problem and \(\alpha^{*}\) and \(\beta^{*}\) are the solution to the dual problem and both outcomes are identical. This allows us to solve the dual problem of Equation \eqref{3-6} instead of the primal problem. Moreover, \(w^{*}\), \(b^{*}\), \(\xi^{*}\), \(\alpha^{*}\) and \(\beta^{*}\) satisfy the Karush-Kuhn-Tucker (KKT) conditions. We will return to those conditions in Section 3.3.
*Note that there are many other similar results that guarantee a zero duality gap.
3.2 Solving dual form
Taken into account the zero duality gap, we wish to find a solution to the dual optimization problem of Equation \eqref{3-6}. Recall that the dual optimization problem is defined as,
\begin{align} \max_{\substack{\alpha,\beta \newline a_i \geq 0, \beta_i \geq 0}} \min_{w, b, \xi} \quad{} \frac{1}{2}|w|^{2} + C\sum_{i}^{m} \xi_i + \sum_{i}^{m} \alpha_i [(1 - \xi_i) - y^{(i)} (w^{T}x^{(i)} + b)] + \sum_{i}^{m} \beta_i (-\xi_i) \tag{3-8} \label{3-8} \end{align}
To find the solution of the problem, we fix \(a\) and \(\beta\) and minimize \(L(w, b, \xi, \alpha, \beta)\) with respect to \(w\), \(b\) and \(\xi\). This can be done by setting the respective derivatives to zero. Subsequently, we can maximize the reduced Lagrangian with respect to \(\alpha\) and \(\beta\).
Taking the derivative of the Lagrangian with respect to \(w\) and setting it to zero gives,
\begin{align} \frac{\delta}{\delta w} L(w, b, \xi, \alpha, \beta) = w - \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)} = 0 \Rightarrow w = \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)} \tag{3-9} \label{3-9} \end{align}
Similarly, taking the derivative of the Lagrangian with respect to the bias and setting it to zero gives,
\begin{align} \frac{\delta}{\delta b}L(w, b, \xi, \alpha, \beta) = - \sum_{i=1}^{m} \alpha_iy^{(i)} = 0 \Rightarrow \sum_{i=1}^{m} \alpha_iy^{(i)} = 0 \tag{3-10} \label{3-10} \end{align}
Finally, taking the derivative of the Lagrangian with respect to the slack variable and setting it to zero gives,
\begin{align} \frac{\delta}{\delta \xi}L(w, b, \xi, \alpha, \beta) = C-\alpha_i-\beta_i = 0 \Leftrightarrow \beta_i = C - \alpha_i \tag{3-11} \label{3-11} \end{align}
Given the dual constraint that \(\beta_i \geq 0\), the above expression leads to a constraint that \(C-\alpha_i \geq 0\) or \(\alpha_i \leq C\). Furthermore, given the dual constraint that \(\alpha_i \geq 0\), we end up with the following constraint on alpha,
\begin{align} 0\leq \alpha_i \leq C, \quad{} \forall i = 1,…,m \tag{3-12} \label{3-12} \end{align}
Now, substituting Equations \eqref{3-9} - \eqref{3-11} back into \(L(w, b, \xi, \alpha, \beta)\) and simplifying allows us to rewrite the Lagrangian only in terms of alpha,
\begin{align} L(a) = \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i,j = 1}^m \alpha_i \alpha_j y^{(i)}y^{(j)} (x^{(i)})^{T} x^{(j)} \tag{3-13} \label{3-13} \end{align}
Recall the constraints on alpha that we obtained in Equation \eqref{3-10} and \eqref{3-12}. Putting this together with the above reduced Lagrangian, we obtain the dual optimization problem:
\begin{equation} \begin{array}{rrclcl} \displaystyle \max_{\alpha} & \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} \alpha_i \alpha_j y^{(i)}y^{(j)} \langle x^{(i)},x^{(j)} \rangle \tag{3-14} \label{3-14} \newline \textrm{subject to} &0 \leq \alpha_i \leq C \quad{} \forall i = 1, …, m \newline & \sum_{i=1}^{m}\alpha_iy^{(i)} = 0 \newline \end{array} \end{equation}
Note that we have replaced \((x^{(i)})^{T}x^{(j)}\) with \(\langle x^{(i)},x^{(j)} \rangle\). This is just the definition of the inner product, and will be useful for the kernelized SVM.
3.3 KKT Conditions and strong duality
If for some \(w^{*}\), \(b^{*}\), \(\xi^{*}\), \(\alpha^{*}\) and \(\beta^{*}\) strong duality holds, then the KKT conditions follow. Moreover, if the KKT conditions hold, then \(w^{*}\), \(b^{*}\), \(\xi^{*}\), \(\alpha^{*}\) and \(\beta^{*}\) are the primal and dual solutions. Thus, the KKT conditions are always sufficient, but necessary under strong duality. The KKT conditions of the given primal and dual problem are as follows:
1: Primal feasibility: the primal constraints hold, i.e.
\(\quad{} y^{(i)} ((w^{*})^{T}x^{(i)} + b^{*}) \geq 1 - \xi_i^{*} \quad{} \forall i = 1, …, m \tag{1.1} \label{1.1}\)
\(\quad{} \xi_i^{*} \geq 0 \quad{} \forall i = 1, …, m \tag{1.2} \label{1.2} \)
2: Dual feasibilitiy: the dual constraints hold, i.e.
\(\quad{} a^{*} \geq 0 \tag{2.1} \label{2.1} \)
\(\quad{} \beta^{*} \geq 0 \tag{2.2} \label{2.2}\)
3: Complimentary slackness, i.e.
\(\quad{} \alpha_{i}^{*} [(1 - \xi_{i}^{*}) - y^{(i)} ( (w^{*})^{T}x^{(i)} + b^{*})] = 0 \quad{} \forall i = 1, …, m \tag{3.1} \label{3.1} \)
\(\quad{} \beta_{i}^{*} ( \text{-} \xi_{i}^{*} ) = 0 \quad{} \forall i = 1, …, m \tag{3.2} \label{3.2} \)
4: Stationarity: the gradient with respect to \(w\), \(b\) and \(\xi\) is zero, i.e.
\( \quad{} \frac{\delta}{\delta w}L(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \beta^{*}) = 0 \tag{4.1} \label{4.1} \)
\( \quad{} \frac{\delta}{\delta b}L(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \beta^{*}) = 0 \tag{4.2} \label{4.2}\)
\(\quad{} \frac{\delta}{\delta \xi}L(w^{*}, b^{*}, \xi^{*}, \alpha^{*}, \beta^{*}) = 0 \tag{4.3} \label{4.3}\)
From these conditions, we can extract some usefull information. In particular,
- If \(\alpha_{i}^{*} = 0 \quad{} \xrightarrow{\text{Eq. } \eqref{3-11}} \quad{} \beta_{i}^{*} = C \quad{} \xrightarrow{\text{Con. } \eqref{3.2}} \quad{} \quad{} \xi_{i}^{*} = 0 \quad{} \xrightarrow{\text{Con. } \eqref{1.1}} \quad{} y^{(i)} ((w^{*})^{T}x^{(i)} + b^{*}) \geq 1 \)
- If \(\alpha_{i}^{*} = C \quad{} \xrightarrow{\text{Eq. } \eqref{3-11}} \quad{} \beta_{i}^{*} = 0 \quad{} \xrightarrow{\text{Con. } \eqref{3.2} \text{, } \eqref{1.2} \text{ and } \eqref{1.1}} \quad{} y^{(i)} ((w^{*})^{T}x^{(i)} + b^{*}) \leq 1\)
- If \(0 < \alpha_{i}^{*} < C \quad{} \xrightarrow{\text{Eq. } \eqref{3-11}} \quad{} \beta_{i}^{*} \in (0,C) \quad{} \xrightarrow{\text{Con. } \eqref{3.2}} \quad{} \xi_{i}^{*} = 0 \quad{} \xrightarrow{\text{Con. } \eqref{3.1}} \quad{} y^{(i)} ((w^{*})^{T}x^{(i)} + b^{*}) = 1\)
Overall, it follows that for \(a_{i}^{*} \in (0,C)\) we have \(y^{(i)} ((w^{*})^{T} x + b^{*}) = 1\). In other words, the non-negative alpha’s ranging between \(0\) and \(C\) have a margin distance from the seperating hyperplane and, thus, must be the support vectors. The direct consequence of this is that we are in a position to easily identify the support vectors from the training set. At the same time, it provides an indicator regarding whether or not the algorithm is overfitting (fewer support vectors indicates a lower VC dimensionality).
3.4 Classification
Suppose we fit the model’s parameters to a training set, extracted the optimal value \(\alpha^{*}\) and now wish to make a prediciton \(\hat{y}\) at a new point \(x\). This would require us to calculate the sign of \((w^{*})^{T}x+b^{*}\). This quantity, however, depends on \(w^{*}\) while the solution to the dual problem gives us the optimal values of alpha. Luckily, we can use Equation \eqref{3-9} to express \(w^{*}\) in terms of \(\alpha^{*}\). In particular, to make a prediction we can take the sign of
\begin{align} (w^{*})^{T}x+b^{*} \Rightarrow (\sum_{i=1}^{m} \alpha_i^{*} y^{(i)} x^{(i)})^{T}x+b^{*} \Rightarrow \sum_{i=1}^{m} \alpha_i^{*} y^{(i)} \langle x^{(i)}, x \rangle + b^{*} \tag{3-15} \label{3-15} \end{align}
Hence, if we’ve found the \(\alpha_i^{*}\)’s, we have to calculate quantities that depend only on the inner products between our new point \(x\) and the examples in the training set. Taken into account that the majority of these \(\alpha_i^{*}\)’s are zero, many of the terms in the sums above will be zero. In turn, we only have to take the inner products between the new point \(x\) and a small set of support vectors to do predictions.
Now, the only thing left to do is to find the optimal value of the bias in terms of alpha. To do so, we consider a support vector (i.e. an unbound example with \(0 < a_{i}^{*} < C\)). According to the complimentary slackness condtions of the previous section, this vector has \(y^{(i)} ((w^{*})^{T} x^{(i)}+ b^{*}) = 1\). Rewriting this in terms of \(b^{*}\) and taking into account that \(y^{(i)} \in \{-1,+1\}\) we get,
\begin{align} b^{*} = \tag{3-16} \label{3-16} \begin{cases} 1 - (w^{*})^{T} x^{(i)} & \quad \text{if } y^{(i)} = 1 \newline -1 - (w^{*})^{T} x^{(i)} & \quad \text{if } y^{(i)} = -1 \newline \end{cases} \end{align}
Or more consicely,
\begin{align}
b^{*} = y^{(i)} - (w^{*})^{T}x^{(i)} \tag{3-17} \label{3-17}
\end{align}
From a numerical stability standpoint, and in particular when taking into account the stopping criteria, the actual value of the margin may not be exactly equal to 1, so generally one averages over the \( b^{*} \) ‘s of all support vectors when performing the calculation. If we denote \( S = \{i|\alpha_{i}^{*}>0\} \) as the set of support vectors, then
\begin{align} b^{*} = \frac{1}{|S|} \sum_{i \in S} [y^{(i)} - (w^{*})^{T}x^{(i)}] \tag{3-18} \label{3-18} \end{align}
where \(|S|\) denotes the number of support vectors in the set. We already derived the optimal value of \(w^{*}\) above, so we could stop here. However, for the purpose of implementing kernelization, we can substitute Equation \eqref{3-9} into the above equation and rewrite it as follows,
\begin{align} b^{*} = \frac{1}{|S|} \sum_{i \in S} [y^{(i)} - (\sum_{j=1}^{m} \alpha_j^{*} y^{(j)} x^{(j)})^{T}x^{(i)}] \tag{3-19} \label{3-19} \end{align}
Finally, we can express the above equation using inner products by distributing the transpose,
\begin{align} b^{*} = \frac{1}{|S|} \sum_{i \in S} [y^{(i)} - \sum_{j=1}^{m} \alpha_j^{*} y^{(j)} \langle x^{(j)}, x^{(i)}\rangle] \tag{3-20} \label{3-20} \end{align}
Note that, just like the objective function in Equation \eqref{3-14}, the optimal bias term as given in Equation \eqref{3-20} depends on the inner product of the training examples with the support vectors. In contrast, the sum in Equation \eqref{3-15} depends on the inner product between the training examples with a new input value \(x\). Despite this subtle difference, we are now in a position to kernelize the dual SVM problem.
Chapter 4: Kernelization
4.1 Kernel trick
In classification problems, it is sometimes the case that the data points are non-linearly seperatable. One remedy is to map the datapoints into a higher dimensional space, in which the data is more likely to be linearly seperatable. The drawback of doing classification in higher dimensional space is the increased computational cost. This difficulty, however, can be overcome if the computation depends exclusively on inner products of vectors. That is, if we can apply a kernel function.
These kernel functions can be regarded as a generalized dot product between two vectors \(x\) and \(y\) in some (possible very) high dimensional feature space. Suppose we have a mapping \(\phi : \mathcal{R}^{n} \rightarrow \mathcal{R}^{m}\) that brings our vectors in \(\mathcal{R}^{n}\) into some higher dimensional feature space \(\mathcal{R}^{m}\). Then the dot product of \(x\) and \(y\) in this higher dimensional feature space is \(\phi(x)^{T} \phi(y)\). A kernel is basically a compressed function \(k\) that corresponds to this dot product,
\begin{align} k(x, y) = \phi(x)^{T} \phi(y) \tag{4-1} \label{4-1} \end{align}
In other words, kernel functions give a way to compute the dot product between \(\phi(x)\) and \(\phi(y)\), without explicitly specifying the so-called kernel-induced implicit mapping \(\phi(\cdot)\).
To elaborate, we will consider one kernel function - the polynomial kernel. This kernel function is defined as follows,
\(k(x, y) = (1+x^{T}y)^{2} \tag{4-2} \label{4-2}\)
At first glance, the above equation looks like a simple expression with some real valued outcome. It does not, at all, seem to correspond to any mapping function \(\phi(\cdot)\).
Without loss of generality, we assume that \(x, y \in \mathcal{R}^{2}\) with \(x = [x_{1}, x_{2}]\) and \(y = [y_{1}, y_{2}]\). This allows us to expand Equation \eqref{4-2} as,
\begin{align} k(x, y) &= (1+x^{T}y)^{2} \Leftrightarrow (1+x_{1} y_{1} + x_{2} y_{2})^{2} \tag{4-3} \label{4-3} \newline & = 1 + x_{1}^{2} y_{1}^{2} + x_{2}^{2} y_{2}^{2} + 2x_{1}y_{1} + 2x_{2}y_{2} + 2x_{1}x_{2}y_{1}y_{2} \end{align}
Note that Equation \eqref{4-3} is nothing else but the dot product between the vectors
\begin{align} \phi(x) = \begin{bmatrix} 1 \newline x_{1}^2 \newline x_{2}^2 \newline \sqrt{2}x_{1} \newline \sqrt{2}x_{2} \newline \sqrt{2}x_{1}x_{2} \end{bmatrix} \quad \text{ and } \quad \phi(y) = \begin{bmatrix} 1 \newline y_{1}^2 \newline y_{2}^2 \newline \sqrt{2}y_{1} \newline \sqrt{2}y_{2} \newline \sqrt{2}y_{1}y_{2} \end{bmatrix} \end{align}
So, the kernel function \(k(x, y) = (1+x^{T} y)^{2} \Leftrightarrow \phi(x)^T \phi(y))\) computes a dot product in 6-dimensional space without explicity setting foot in it.
Other examples of kernel functions include the linear kernel, exponential kernel, the radial basis function, and, the most popular, Gaussian kernel. The latter is defined as \(k(x,y) = \text{exp} (- \gamma |x-y|^2)\) and corresponds to an infinite-dimensional mapping.
4.2 Kernelized SVM
The kernel-trick can be applied to the SVM algorithm considered previously because all the data points appear in the algorithm by means of an inner product. To apply the kernel trick, during the training process, we replace the inner product \(\langle x^{(i)}, x^{(j)} \rangle \) of Equation \eqref{3-14} by a kernel function \(k(x^{(i)}, x^{(j)})\) to get,
\begin{equation} \begin{array}{rrclcl} \displaystyle \max_{\alpha} & \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} \alpha_i \alpha_j y^{(i)}y^{(j)} k(x^{(i)},x^{(j)}) \tag{4-4} \label{4-4} \newline \textrm{subject to} &0 \leq \alpha_i \leq C \quad{} \forall i = 1, …, m \newline & \sum_{i=1}^{m}\alpha_iy^{(i)} = 0 \newline \end{array} \end{equation}
Similarly, after finding the optimal alpha values, we classify new examples by replacing the inner product inside of Equation \eqref{3-15} with the kernel function,
\begin{align} f(x) = \sum_{i=1}^{m} y^{(i)} \alpha_{i}^{*} k(x_{i}, x) + b^{*} \tag{4-5} \label{4-5} \end{align}
where \(b^{*}\) is defined as
\begin{align} b^{*} = \frac{1}{|S|} \sum_{i \in S} [y^{(i)} - \sum_{j=1}^{m} \alpha_j^{*} y^{(j)} k(x^{(j)}, x^{(i)})] \tag{4-6} \label{4-6} \end{align}
Note that kernel methods are not SVM exclusive. In fact, the kernel method can be used on any algorithm that is based on solely inner products of vectors. One example is the kernel principal component analysis (KPCA).
Chapter 5: SMO algorithm
5.1 Update rule
As derived in the previous section, the QP problem to train an SVM is given by,
\begin{equation} \begin{array}{rrclcl} \displaystyle \max_{\alpha} & \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} \alpha_i \alpha_j y^{(i)}y^{(j)} k(x^{(i)},x^{(j)}) \tag{5-1} \label{5-1} \newline \textrm{subject to} &0 \leq \alpha_i \leq C \quad{} \forall i = 1, …, m \newline & \sum_{i=1}^{m}\alpha_iy^{(i)} = 0 \newline \end{array} \end{equation}
where \(k(x^{(i)},x^{(j)})\) is the kernel function.
To solve the kernelized SVM problem, we apply the so-called Sequential Minimal Optimization algorithm (or, abbreviated, “SMO”). The SMO breaks the large QP problem into a series of smallest possible QP problems. These small QP problems are solved analytically, which avoids using a time-consuming numerical QP optimization as an inner loop. At every step, the SMO chooses two Lagrange multipliers to jointly optimize, finds the optimal values for these multipliers, and updates the SVM to reflect the new optimal values.
Without loss of generality, let the two multipliers we try to optimize be \(\alpha_1\) and \(\alpha_2\). When we optimize two variables at a time, the objective function can be obtained by dropping all constant terms independent of the two selected variables \(\alpha_1\) and \(\alpha_2\) in the original objective function. That is,
\begin{equation} \begin{array}{rrclcl} \displaystyle \max_{\alpha_1, \alpha_2} & \alpha_1 + \alpha_2 - \frac{1}{2} (\alpha_1^2 K_{11} + \alpha_2^{2} K_{22} + 2a_{1}a_{2}y^{(1)}y^{(2)}K_{12}) \newline &\quad{} - \alpha_1 y^{(1)} \sum_{j \neq 1, 2}^{m} \alpha_j y^{(j)} K_{1j} - \alpha_2 y^{(2)} \sum_{i \neq 1, 2}^{m} \alpha_i y^{(i)} K_{i2} \tag{5-2} \label{5-2} \newline \textrm{subject to} & \alpha_{1} y^{(1)} + \alpha_2 y^{(2)} = - \sum_{i \neq 1,2}^{m} \alpha_{i} y^{(i)} \newline & 0 \leq a_1, a_2 \leq C \end{array} \end{equation}
where we simplify the notation for the kernal function with \(K_{nm} = k(x_m, x_n)\). Note that the constraint is rewritten as,
\begin{align} \sum_{i=1}^{m} a_i y^{(i)} = 0 \Leftrightarrow \alpha_1 y^{(1)} + \alpha_2 y^{(2)} = -\sum_{i \neq 1,2}^m \alpha_i y^{(i)} \tag{5-3} \label{5-3} \end{align}
By multiplying both sides of Equation \eqref{5-3} by \(y^{(1)} \in \{-1, 1\}\), we get:
\begin{align} \alpha_1 (y^{(1)})^{2} + (y^{(1)} y^{(2)}) \alpha_2 = \alpha_1 + s \alpha_2 = (-\sum_{i \neq 1,2}^m \alpha_i y^{(i)}) y^{(1)} = \zeta \Leftrightarrow \alpha_1 + s \alpha_2 = \zeta \tag{5-4} \label{5-4} \end{align}
where we define \(s = y^{(1)} y^{(2)}\) and \(\zeta = (-\sum_{i \neq 1,2}^m \alpha_i y^{(i)}) y^{(1)}\), which both remain the same before and after \(\alpha_{1}\) and \(\alpha_{2}\) get updated. This implies that \(\alpha_{1}^{new} + s \alpha_{2}^{new} = \alpha_{1}^{old} + s \alpha_2^{old} = \zeta\) and therefore \(\alpha_1^{new} = \alpha_1^{old} + s (\alpha_2^{old} - \alpha_2^{new})\). We can later use this expression to derive an update rule between the \(\alpha_{2}^{old}\) and the optimal value \(\alpha_{2}^{new}\) as well as to go back and forth between \(\alpha_{1}^{new}\) and \(\alpha_{2}^{new}\) after we derived the optimal value for one of them.
We now consider a closed-form solution for updating \(\alpha_1\) and \(\alpha_2\). To do so, we rewrite the summations in the last two terms of Equation \eqref{5-2} as \(\upsilon_{k}\) with \(k=1,2\). In particular,
\begin{align} \upsilon_{k} & = \sum_{i\neq 1,2} ^{m} \alpha_i y^{(i)} K_{ik} \tag{5-5} \label{5-5} \newline &\quad = \sum_{i}^{m} \alpha_i y^{(i)} K_{ik} - \alpha_{1}y^{(1)}K_{1k} - \alpha_{2}y^{(2)}K_{2k} \newline &\quad = (\sum_{i}^{m} \alpha_i y^{(i)} K_{ik} +b) - b - \alpha_{1}y^{(1)}K_{1k} - \alpha_{2}y^{(2)}K_{2k} \newline &\quad = \rho_k - b - \alpha_{1}y^{(1)}K_{1k} - \alpha_{2}y^{(2)}K_{2k} \newline \end{align}
where \(\rho_{k} = \sum_{i}^{m} \alpha_i y^{(i)} K_{ik} +b\) is the output of the kernelized decision function of Equation \eqref{4-5} with \(x^{(k)}\) as the input value. Note that \(\upsilon_{k}\) is independent of the update of the Lagrangian multipliers \(\alpha_{1}\) and \(\alpha_{2}\). That is, we can express \(\upsilon_{k}\), and therefore \(\rho_{k}\), using only old values of alpha. From this, it follows that \(\rho_{k} = \sum_{i}^{m} \alpha_{i}^{old} y^{(i)} K_{ik} + b\).
Using Equation \eqref{5-5}, the objective function of Equation \eqref{5-2} can be simplified to:
\begin{align} L(\alpha_1, \alpha_2) = \alpha_1 + \alpha_2 - \frac{1}{2} (\alpha_1^2 K_{11} + \alpha_2^{2} K_{22} + 2a_{1}a_{2}y^{(1)}y^{(2)}K_{12}) - \alpha_1 y^{(1)} \upsilon_1 - \alpha_2 y^{(2)} \upsilon_2 \tag{5-6} \label{5-6} \end{align}
Our goal is to find the optimal values \(\alpha_1^{*}\) and \(a_2^{*}\) that maximize the above objective function. To do so, we first express it as a function of \(\alpha_{2}\) alone by substituting \(\alpha_1 = \zeta - s \alpha_2\) from Equation \eqref{5-4} into \eqref{5-6}. That is,
\begin{align} L(\alpha_2) & = [\zeta - s \alpha_2] + \alpha_2 - \frac{1}{2} ([\zeta - s \alpha_2]^2 K_{11} + \alpha_2^{2} K_{22} + 2 [\zeta - s \alpha_2] \alpha_{2}y^{(1)}y^{(2)}K_{12}) \tag{5-7} \label{5-7} \newline &\quad - [\zeta - s \alpha_2] y^{(1)} \upsilon_1 - \alpha_2 y^{(2)} \upsilon_2 \newline & = \zeta + \alpha_2 (1 - s) - \frac{1}{2} [\zeta - s \alpha_2]^2 K_{11} - \frac{1}{2} \alpha_2^{2} K_{22} - [\zeta - s \alpha_2] \alpha_{2} s K_{12} \newline &\quad - [\zeta - s \alpha_2] y^{(1)} \upsilon_1 - \alpha_2 y^{(2)} \upsilon_2 \newline & = \zeta + \alpha_2 (1 - s) - \frac{1}{2} (\zeta - s \alpha_{2})(\zeta - s \alpha_{2}) K_{11} - \frac{1}{2} \alpha_{2}^{2} K_{22} - \zeta \alpha_{2} s K_{12} + \alpha_{2}^{2} s^{2} K_{12} \newline &\quad - \zeta y^{(1)} \upsilon_{1} + s \alpha_{2} y^{(1)} \upsilon_{1} - \alpha_{2} y^{(2)} \upsilon_{2} \newline & = \zeta + \alpha_{2}(1-s) - \frac{1}{2} \zeta^{2} K_{11} + s \alpha_{2} \zeta K_{11} - \frac{1}{2} s^{2} \alpha_{2}^2 K_{11} - \frac{1}{2} \alpha_{2}^{2} K_{22} - \zeta \alpha_{2} s K_{12} + \alpha_{2}^{2} s^{2} K_{12} \newline &\quad - \zeta y^{(1)} \upsilon_{1} + s \alpha_{2} y^{(1)} \upsilon_{1} - \alpha_{2} y^{(2)} \upsilon_{2} \newline & = (1 - s + \zeta s K_{11} -\zeta s K_{12} + s y^{(1)}\upsilon_{1} - y^{(2)}\upsilon_{2}) \alpha_{2} + \frac{1}{2} (-s^{2} K_{11} - K_{22} + 2s^{2}K_{12}) \alpha_{2}^{2} \newline &\quad - (\frac{1}{2} \zeta^{2} K_{11} + \zeta y^{(1)} \upsilon_1) \newline & = (1 - s + \zeta s K_{11} -\zeta s K_{12} + y^{(1)} y^{(2)} y^{(1)}\upsilon_{1} - y^{(2)}\upsilon_{2}) \alpha_{2} + \frac{1}{2} (-s^{2} K_{11} - K_{22} + 2s^{2}K_{12}) \alpha_{2}^{2} + c \newline & = (1 - s + \zeta s (K_{11} - K_{12}) + y^{(2)} (\upsilon_{1} - \upsilon_{2})) \alpha_{2} + \frac{1}{2} (2K_{12} - K_{11} - K_{22}) \alpha_{2}^{2} + c \end{align}
where \(c\) is a constant that does not depend on \(\alpha_{1}\) and \(\alpha_{2}\). Hence, we are free to remove it from our objective function. Using Equation \eqref{5-7}, we can now identify and simplify the coefficient of the quadratic term \(\alpha_{2}^{2}\) as follows,
\begin{align} \frac{1}{2} (2K_{12} - K_{11} - K_{22}) & \Leftrightarrow \frac{1}{2} \eta \quad{} \tag{5-8} \label{5-8} \end{align}
where,
\begin{align} \eta &= 2K_{12} - K_{11} - K_{22} \Leftrightarrow 2z_{1}^Tz_{2} - z_{1}^Tz_{1} - z_{2}^Tz_{2} \Leftrightarrow -(z_{1}^T-z_{2}^{T}) (z_{1} - z_{2}) \Leftrightarrow \tag{5-9} \label{5-9} \newline &\quad -(z_{1}-z_{2})^T(z_{1}-z{2}) \Leftrightarrow - |z_{1}-z_{2}|^{2} \leq 0 \end{align}
where \(z_{k} = \phi(x_{k})\).
Similarly, using Equation \eqref{5-7}, we can simplify the coefficient of the linear term \(\alpha_{2}\). In particular, using \(\zeta = \alpha_1^{old} + s\alpha_2^{old}\) and \(\upsilon_k\) from the discussions surrounding Equation \eqref{5-4} and \eqref{5-5}, respectively, the coefficient of \(\alpha_2\) is given by,
\begin{align} &\quad{} = 1 - s + \zeta s (K_{11} - K_{12}) + y^{(2)} (\upsilon_{1} - \upsilon_{2}) \tag{5-10} \label{5-10} \newline &\quad{} = 1 - s + s(\alpha_{1} + s \alpha_{2})(K_{11} - K_{12}) + y^{(2)} (\upsilon_{1} - \upsilon_{2}) \newline &\quad{} = 1 - s + (s\alpha_{1} + \alpha_{2})(K_{11} - K_{12}) + y^{(2)} (\rho_1 - b - \alpha_{1} y^{(1)} K_{11} - \alpha_{2} y^{(2)} K_{21} - \rho_2 + b + \alpha_{1} y^{(1)} K_{12} + \alpha_{2}y^{(2)} K_{22}) \newline &\quad{} = 1 - s + y^{(2)} (\rho_1 - \rho_2) + s\alpha_{1} K_{11} - s \alpha_{1} K_{12} + \alpha_{2} K_{11} - \alpha_{2} K_{12} - s \alpha_{1} K_{11} - \alpha_{2} K_{21} + s \alpha_{1} K_{12} + \alpha_{2} K_{22} \newline &\quad{} = 1 - s + y^{(2)} (\rho_1 - \rho_2) - \alpha_{2} (2K_{12} - K_{11} - K_{22}) \newline &\quad{} = (y^{(2)})^2 - y^{(1)}y^{(2)} + y^{(2)} (\rho_{1} - \rho_{2}) - \alpha_{2} \eta \newline &\quad{} = y^{(2)} (\rho_{1} - y^{(1)} - (\rho_{2} -y^{(2)})) - \alpha_{2} \eta \newline &\quad{} = y^{(2)} (E_{1} - E_{2}) - \alpha_{2}^{old} \eta \end{align}
where \(E_{k} = \rho_{k} - y^{(k)} \Leftrightarrow \sum_{i=1}^{m}a_{i}^{old} y^{(i)}K_{ik} + b - y^{(k)}\) is the difference between the desired output \(y_{k}\) and the actual output based on the previous values of the alpha values. For the sake of clarity we supressed the “old” superscript untill the last line of derivation.
Using Equation \eqref{5-8} and \eqref{5-10}, we can rewrite the quadratic objective function of Equation \eqref{5-7} as
\begin{align} L(\alpha_{2}) = [\frac{1}{2} \eta] \alpha_{2}^{2} + [y^{(2)} (E_{1} - E_{2}) - \alpha_{2}^{old} \eta] \alpha_{2} \tag{5-11} \label{5-11} \end{align}
To maximize the objective function, we consider the first- and second order derivative as follows:
\begin{align} \frac{\delta}{\delta \alpha_{2}} L(\alpha_{2}) & = \eta \alpha_{2} + y^{(2)} (E_{1} - E_{2}) - \alpha_{2}^{old} \eta \tag{5-12} \newline \frac{\delta^{2}}{\delta^{2} \alpha_{2}} L(\alpha_{2}) & = \eta \leq 0 \tag{5-13} \label{5-13} \newline \end{align}
Given that the SOC is non-positive, we know it has a maximum. Thus, the FOCs provide us with the point \(\alpha_{2}\) that maximizes \(L(\alpha_{2})\) based on the old value \(\alpha_{2}^{old}\). In particular,
\begin{align} \frac{\delta}{\delta \alpha_2} L(\alpha_2) = 0 \Leftrightarrow \eta \alpha_{2} + y^{(2)} (E_{1} - E_{2}) - \alpha_{2}^{old} \eta = 0 \Leftrightarrow \alpha_{2}^{new} = \alpha_{2}^{old} - \frac{y^{(2)} (E_{1} - E_{2})}{\eta} \tag{5-14} \label{5-14} \end{align}
where \(\alpha_{2}^{new}\) denotes the unconstrained optimal value of \(\alpha_{2}\).
5.2 Parameter clipping
The optimal value of the alpha that we found in the previous section is unconstrained. That is, it does not necessarily satisfiy the constraints from Equation \eqref{5-2}. To assure that the alphas satisfiy these constraints, we clip its values.
Recall that the linear equality constraint in Equation \eqref{5-2} requires the Lagrange multipliers to lie on the diagonal line \(\alpha_{1} + s\alpha_{2} = \zeta\), where we can interpret \(\zeta\) as the bias term. Furthermore, the bound constraints in Equation \eqref{5-2} requires the Lagrange multipliers to lie within the box \([0,C] \text{ x } [0,C]\). Thus, both constraints imply that the constrained maximum of the objective function must lie on a diagonal line segment.
Overall, as demonstrated in Fig. 6 and 7, there will be some lower-bound \(L\) and some upper-bound \(U\) on the permissible values for \(\alpha_{2}\) that will ensure that \(\alpha_{1}\) and \(\alpha_{2}\) lie on this diagonal line segment. In particular, we can distinguish between four subcases.
Figure 6: Lower and upperbound if \(s = 1\), i.e. the line is downward sloping
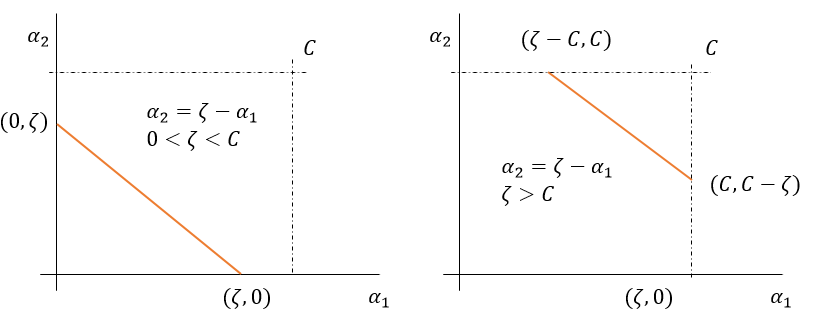
If \(s = 1\) (Fig 6) then \(\alpha_1 + s\alpha_2 = \zeta \Rightarrow \alpha_2 = \zeta - \alpha_1\), i.e. the line is downward sloping. Moreover,
- If \(0 < \zeta < C\) (left) then \(\min(\alpha_2)\) is at \(\alpha_{2} = 0\) and \(\max(\alpha_{2})\) is at \(\alpha_1 = 0 \Rightarrow \alpha_2 = \zeta\).
- If \(\zeta > C\) (right) then \(\min(\alpha_2)\) is at \(\alpha_1 = C \Rightarrow \alpha_2 = \zeta - C\) and \(\max(\alpha_2)\) is at \(\alpha_2 = C\).
Combined this implies that,
\begin{align} \tag{5-15} \label{5-15} \begin{cases} L = \max(0, \zeta - C) = \max(0, \alpha_{1} + \alpha_{2} - C) \newline U = \min(\zeta, C) = \min(\alpha_{1} + \alpha_{2}, C) \newline \end{cases} \end{align}
Figure 7: Lower and upperbound if \(s = -1\), i.e. the line is upward sloping
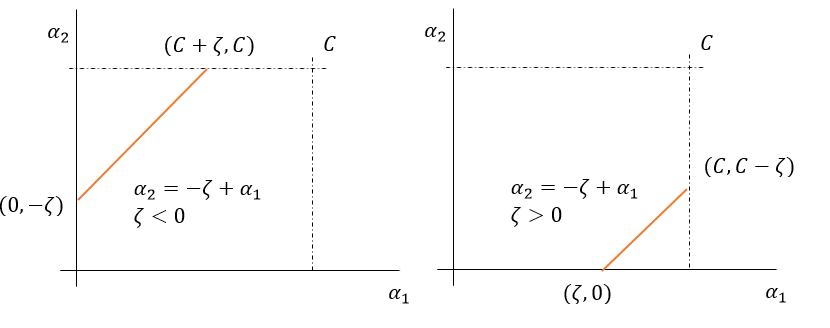
On the other hand, if \(s = -1\) (Fig. 7), then \(\alpha_1 + s\alpha_2 = \zeta \Rightarrow \alpha_2 = -\zeta + \alpha_1\), i.e. the line is upward sloping. Moreover,
- If \(\zeta < 0\) (left) then \(\min(\alpha_{2})\) is at \(\alpha_1 = 0 \Rightarrow alpha_2 = -\zeta\) and \(\max(\alpha_2)\) is at \(\alpha_2 = C\).
- If \(0 < \zeta < C\) (right) then \(\min(\alpha_2)\) is at \(\alpha_2=0\) and \(\max(\alpha_2)\) is at \(\alpha_1 = C \Rightarrow \alpha_2 = -\zeta + C\).
Combined this implies that,
\begin{align} \tag{5-16} \label{5-16} \begin{cases} L = \max(0, -\zeta) = \max(0, \alpha_1 - \alpha_2) \newline U = \min(C - \zeta, C) = \min(C - \alpha_1 + \alpha_2, C) \newline \end{cases} \end{align}
Thus, now we can apply the diagonal line segment constraints to the optimal unconstrained solution \(\alpha_{2}^{new}\) derived in Section 5.1. In particular,
\begin{align} \alpha_{2}^{new, clipped} = \tag{5-17} \label{5-17} \begin{cases} U &\quad{} \text{if } \alpha_{2}^{new} \geq U \newline \alpha_{2}^{new} &\quad{} \text{if } L < \alpha_{2}^{new} < U \newline L &\quad{} \text{if } \alpha_{2}^{new} \leq L \newline \end{cases} \end{align}
Finally, we can use \(\alpha_1^{new} = \alpha_1^{old} + s (\alpha_{2}^{old} - \alpha_{2}^{new \text{, } clipped})\) from our discussion surrounding \eqref{5-4} to find the (constrained) optimal value of \(\alpha_{1}\).
5.3 Selecting the threshold
The update rule for alpha, as given in Equation \eqref{5-14}, depends on the error term \(E_{k}\) and, in turn, on the value of \(b\). Thus, to update the value of the error cache at the end of each iteration, we need to re-evalute the value of \(b\) after each optimization.
Using the error term utilized in Equation \eqref{5-10}, we consider the following equality,
\begin{align} E_{k}^{new} - E_{k}^{old} & = (\rho_{k}^{new} - y^{(k)}) - (\rho_{k}^{old} - y^{(k)}) \tag{5-18} \label{5-18} \newline & = \rho_{k}^{new} - \rho_{k}^{old}\newline & = (\sum_{i=1}^{m} \alpha_{i}^{new} y^{(i)} K_{ik} + b^{new}) - (\sum_{i=1}^{m} \alpha_{i}^{old} y^{(i)} K_{ik} + b^{old}) \newline & = \sum_{i=1}^{m} a_{i}^{new} y^{(i)} K_{ik} - \sum_{i=1}^{m} a_{i}^{old} y^{(i)} K_{ik} + b^{new} - b^{old} \newline & = \sum_{i\neq 1,2}^{m} \alpha_{i}^{new} y^{(i)} K_{ik} + \sum_{i = 1,2} a_{i}^{new} y^{(i)} K_{ik} - \sum_{i\neq 1,2}^{m} \alpha_{i}^{old} y^{(i)} K_{ik}-\sum_{i = 1,2} \alpha_{i}^{old} y^{(i)} K_{ik} + b^{new}-b^{old} \newline & = \sum_{i = 1,2} a_{i}^{new} y^{(i)} K_{ik} - \sum_{i = 1,2} \alpha_{i}^{old} y^{(i)} K_{ik} + b^{new} - b^{old} \newline & = (\alpha_{1}^{new} y^{(1)} K_{1k} + \alpha_{2}^{new} y^{(2)} K_{2k}) - (\alpha_{1}^{old} y^{(1)} K_{1k} + \alpha_{2}^{old} y^{(2)} K_{2k}) + b^{new} - b^{old} \newline & = (a_{1}^{new} - \alpha_{1}^{old}) y^{(1)} K_{1k} + (\alpha_{2}^{new, clipped} - \alpha_{2}^{old}) y^{(2)} K_{2k} + b^{new} - b^{old} \newline \end{align}
For the sake of clarity we supressed the “clipped” superscript untill the last line of derivation.
Now, consider the following scenarios,
- If \(0 < \alpha_{1} < C\) for k = 1 or k = 2 then \(y^{(k)} E_{k}\) should equal 0 according to the KKT conditions.* Taken in mind that \(y^{(k)} \in \{-1, 1\}\), we need \(E_{k}^{new}\) to equal zero for this to hold true. Substituting this into Equation \eqref{5-18} yields,
\begin{align} 0 - E_{k}^{old} & = (\alpha_{1}^{new} - \alpha_{1}^{old}) y^{(1)} K_{1k} + (\alpha_{2}^{new} - \alpha_{2}^{old}) y^{(2)} K_{2k} + b_{k}^{new} - b_{k}^{old} \quad{} (k = 1 \text{or } 2) \tag{5-19} \label{5-19}\newline b_k^{new} & = - E_{k}^{old} - (a_{1}^{new} - a_{1}^{old}) y^{(1)} K_{1k} - (a_{2}^{new} - a_{2}^{old}) y^{(2)} K_{2k} + b_{k}^{old} \newline \end{align}
- If both \(\alpha_{1}\) and \(\alpha_{2}\) are both at the bounds (well away from margin), then anything between \(b_{1}\) and \(b_{2}\) works, so we set, \(b = (b_{1} + b_{2})/2\).
* Note that \(y^{(k)} E_{k} = 0 \Leftrightarrow y^{(k)} (\sum_{i=1}^{m} \alpha_{i} y^{(i)} K_{ik} + b - y^{(k)}) = 0 \Leftrightarrow y^{(k)} f(x^{(k)}) - 1 = 0 \Leftrightarrow y^{(k)} f(x^{(k)}) = 1\). This is exactly the KKT condition if \(0 < a_{k} < C\).
5.4 Python implementation
The python code for the main part of the SMO algorithm is listed below. There are several existing libraries designed specifically for solving the optimization problem(s) presented by SVMs such as LIBLINEAR/LIBSVM and CVXOPT. These libraries should be favored over the implementation below, which is solely meant to be a personal reference or educational resource.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
x, y = make_blobs(n_samples=1000, centers=2, n_features=2, random_state=1)
y = y.reshape(1000,1) # prevents us from working with 1-rank array
y[y == 0] = -1
m, n = x.shape[0], x.shape[1]
alpha = np.zeros((m,1)) # initialize alpha variables
b = 0.0 # initialize bias term
iteration = 0 # interation counter
max_iter = 200 # maximum number of iterations
C = 1000.0 # penalty term
epsilon = 1e-8 # tolerance for KKT violation
while iteration < max_iter:
iteration += 1 # add one to number of iters
alphas_changed = 0 # number of alphas changed counter
alpha_prev = np.copy(alpha)
for i in range(0, m): # for each alpha_i
for j in range (0, m): # for each alpha_j
while j == i: # take an alpha_j =/= alpha_j
j = int(np.random.uniform(0,m))
xi, xj, yi, yj = x[i,:], x[j,:], y[i], y[j]
ai, aj = alpha[i], alpha[j] # store old alpha values
eta = 2 * np.dot(xi, xj.T) - np.dot(xi, xi.T) - np.dot(xj, xj.T)
Ei = (np.sign(np.dot(np.multiply(alpha, y).reshape(1,m), np.matmul(x, xi.T).reshape(m,1)) + b) - yi).astype(int)
Ej = (np.sign(np.dot(np.multiply(alpha, y).reshape(1,m), np.matmul(x, xj.T).reshape(m,1)) + b) - yj).astype(int)
yE = yj*Ej
if (0>alpha[j]>C and epsilon>yE>-epsilon): # at the optimum, the KKT conditions are satisfied
continue
if eta == 0: # ambiguous whether there is a maximum (i.e. SOC /< 0)
continue
if (yi == yj):
L = max(0, ai + aj - C)
H = min(C, ai + aj)
elif (yi != yj):
L = max(0, aj - ai)
H = min(C, C - ai + aj)
if (L==H): # straight line and no improvement possible.
continue
alphaj = aj - float(yj * (Ei - Ej)/eta) # update alphas
if alphaj < epsilon:
alphaj = 0
elif alphaj > C - epsilon:
alphaj = C
if alphaj >= H:
alphaj = H
elif alphaj <= L:
alphaj = L
alpha[j] = alphaj
alpha[i] = ai + yi * yj * (aj-alphaj)
bi = b + Ei + yi * (ai-alpha[i]) * np.dot(xi, xi.T) + yj * (aj - alpha[j]) * np.dot(xi, xj.T)
bj = b + Ej + yi * (ai-alpha[i]) * np.dot(xi, xj.T) + yj * (aj - alpha[j]) * np.dot(xj, xj.T)
if (0 < alpha[i]) and (alpha[i] < C):
b = bi
elif (0 < alpha[j]) and (alpha[j] < C):
b = bj
else:
b = (bi + bj) * 0.5
alphas_changed = alphas_changed + 1
print(alphas_changed)
diff = np.linalg.norm(alpha - alpha_prev) # convergence check
if diff < epsilon:
break
if alphas_changed == 0: # stop if no alphas are changed after one full iteration
break
index = np.where((alpha>0) & (alpha<C))[0] # indicies of non-zero alphas
asv = alpha[index,:] # support vector a-values
xsv = x[index,:] # support vector x-values
ysv = y[index,:] # support vector y-values
nsv = len(ysv)
# Final model parameters
w = np.dot(xsv.T, np.multiply(asv,ysv))
b = np.mean(ysv - np.dot(w.T, xsv.T).T)
# Prediction
x1_1 = min(x[:,0])
x1_2 = max(x[:,0])
ones = np.where((y == 1))[0]
nones = np.where((y == -1))[0]
# Plot
fig, ax = plt.subplots()
colors = {1:'red', -1:'blue'}
ax.scatter(x[ones,0], x[ones,1], c = 'red')
ax.scatter(x[nones,0], x[nones,1], c = 'blue')
plt.plot([x1_1, x1_2], [-(w[0,:]*x1_1 +b)/w[1,:], -(w[0,:]*x1_2 +b)/w[1,:]])
plt.show()
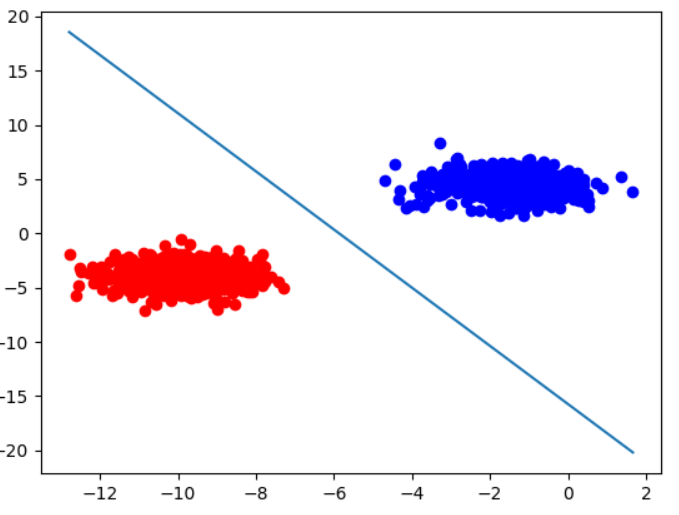
Running the above code yields the following linear seperation:
Figure 7: SVM with linear kernel

Leave a comment